Last edited 2apr14, 23apr14


\begin{document}

Jump to Part II 
\maketitle
Syllabus "Post-Euclidian Geometry"
 
 MA402 Spring 2014 

Instructions 
This file is frequently updated. Check the date and reload your browser

pages each time you visit. Note the convention that "F1" means
"Friday of Week 1".
Label all course submissions by this week-day code as marked "due" 
in the syllabus. 
Square brackets identify the section(s) in Hvidsten's
text which most closely correspond to the lesson. The lessons are labelled by 
section and number, e.g. "C2" for the second lesson in 
 Cartesian Geometry.  
This syllabus overrides all other instructions, in case of an inadvertent conflict. 

 Part I of the Course 

Geometry and the Axiomatic Method [Hvidsten Chapter 1] 

\begin{itemize}
\item W1 [1.1, 1.2] Lesson A1:  Greek Geometry from Thales to Pappus  with associated Filecard due before class F1. 
\item F1 Lesson A2:  Exterior Angle Lab  I  Introduction to Geometry Explorer (GEX2.0) with filecard due before class M2. (Lab report is due in 3 weeks.)  
\item Homework for M2: Read Introduction to Post-Modern Geometry .  
\item Homework for M2: Browse  Advice for Completing this Course. Mark this link to consult throughout the course.
\item M2 Lessons on   Mathematical Typesetting  as discussed in Advice. General Administrivia and Introduction to the Course.
\item W2 Lesson A3:  Axiomatic Systems in Geometry   
\item W2 [1.4] Lesson A4:  Toy Axiom System  better known as Finite Geometries. Filecard is due before class. 
\item F2 Lesson A5:  Exterior Angle Lab  II . Introduction to models of non-Euclidean geometry.
\item M3 [1.5] Lesson A6: Models of Axiomatic Systems .
\item W3 Submit  HomeworkM3 on axiomatic systems on Moodle. Do Hvidsten 1.5.4, 1.5.5., 1.5.6, 1.5.7 as directed, using models. 

\item F3 Review and  Sample Quiz 
\item M4 QuizA. This quiz tests lessons A1-A6 and elementary skills GEX2.0. Be sure to bring your Journal to class with you.   
\end{itemize} 
Euclid's Geometry [Hvidsten Chapter 2] 
\begin{itemize}
\item  W4 [2.1] Lesson E1 on Absolute Geometry  with filecard. 
\item F4 [2.2] Lesson E2 on Euclid's Parallel Postulate   with filecard.
\item M5 [2.3] Lesson E3 on John Playfair's Axiom  and its equivalents. Filecard TBA.
\item W5 Submit HomeworkM5 on Euclid's Parallel Postulate as posed in Lesson E2. 
\item F5 Lesson E4 on the Pythagorean Theorem  as Euclid proved it. Has filecard.
\item W5 Review   
\item M6 QuizE . This is an in-class quiz testing lessons
E1--E3 on Euclid's geometry.
\end{itemize}
 Cartesian Geometry a.k.a. Analytic Geometry.
\begin{itemize}
\item W6   [2.5] Lesson C1 on  Similarity , ladder lemma, AAA, and simSAS. 
\item F6     Lesson C2  on  Cartesian Geometry as Model for Birkhoff's Axioms  
\item F6     Lesson C3  on  Circular Numbers  needed for Birkhoff's Protractor Axiom.
\item F6     Submit  HomeworkF6  on Birkhoff's Axioms. 
\item M7     Advice on preparing for the  Midterm 
\item W7 Midterm  
\end{itemize}


 Part II of the Course 

The second 8 weeks of this course deals with the modern approach to 
geometry in terms of Transformation Groups, in particular the group of 
Moebius Transformation and its subgroups. The Syllabus will be filled 
in as lessons become ready and relevant. Please consult the Syllabus 
daily and be sure to update your browser.



\begin{itemize}
\item F7  Overview of Lessons on Models, Part I.
\item M8 [3.5] The Complex Plane and 
Euler's Theorem. Filecard Z1 questions due.  
\item W8 Discussion of Midterm. 
\item F8 Lesson on  Moebius Transformations . 
Filecard Z2 is due.   
\item M9 Q/A on 
Problems 3.5.1 -- 3.5.5  in Hvidsten.  
\item W9 Lesson on  Cross Ratios  with filecard Z3
\item F9 No Class.
\item M10  Discussion of the Exercises 8.2.1-15
\item W10 Submit Exercises 8.2.8, 8.2.2, and 8.2.3, and the two extensions. 
<\item W10  Supplement  for reference,
as discussed in this session.
\item W10 Lesson on  Hyperbolic Group  with filecard H1.
\item F10 Sample Quiz  on Moebius Transformations.
\item M11 Lesson on  Hyperbolic Distance  with filecard H2.
\item W11 QuizZ . This is an in-class quiz testing lessons Z1, Z2, Z3, H1, on the geometry of the Euclidean plane using complex numbers and M\"obius Transformations. 
\item F11 Lesson on  Hyperbolic Translation  with filecard H3.
\end{itemize}

 Area Hyperbolic Triangle  is its Angular Defect  
\begin{itemize}
\item M12 Gauss' theorem on areas 
\item W12 Gauss' theorem cont'd
\item F12 Review of Lessons H1,H2,H3 (sample quiz).
\item M13 QuizH is postponed  
\item M13 Gauss' theorem concluded.
\end{itemize}

 Isomorphism between Models of Hyperbolic Geometry 
\begin{itemize}
\item W13  Three Equivalent Models 
\item W13  HyperSpace (for macs) 
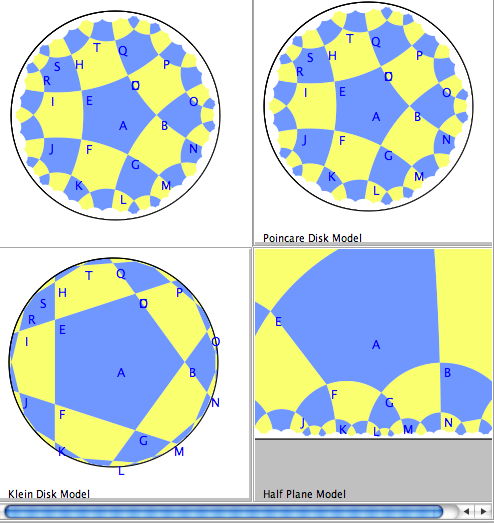
\item W13  Poincare-Klein sketch 
\item F13 Takehome Quiz H  is due M14. It is posted on the Moodle. If you did not get a Moodle notification, or you cannot access the Moodle, you must email me immediately.
\item F13 Equivalence theorem for the various models.
\item M14 Review of the second half of the course.
\item W14 Review of Axiomatic Methods, Absolute Geometry, and Playfair.
\item F14 Review of Euclidean and Cartesian Geometry. Essay topics on final.
\item M15 Return tests and back homework.
\item W15 Private consultations, see signup sheet.
\item F15 Final Exam, 1:30 - 4:30 pm, 24 IH.
\item R16 Conflict Final. 7:00-10:00 pm, 24IH. Consult with me to establish a conflict.
\end{itemize}








\end{document}